«

[Mighty Midget]

If

angle ABC = a (alpha)

K = sin BAC / sin CAD and
L = 180 - (BAC + CAD)

then

K = sin a / sin (L - a)

the solution will be at

sin a / sin (L - a) - K = 0

(tested and verified* with a graphical calculator)

* verified as in I didn't get any wrong answers with several different, arbitrary values for BAC and CAD.

Now is the problem, I am unable to isolate alpha in sin (L - a)
If you can do that, you have the formula, I believe.

[GTX2GvO]

Well ACTUALLY...

As long as the Angles @ A (or just one of) are known and E is a known value.. (Which is in the IRL issue) I just need the KNOWN value of either another angle or another side (c {AC})

Cause with the Law of sines and the 180 degrees rule I can then calculate ALL the other sides/angles..
(If I'm in the mood for it AND have my equipment @ hand)

[Mighty Midget]

The segments at E are, unfortunately, unknown. The only known values are the two angles at A (angle BAC and CAD).

EDIT: Summary

When the function f(a) = sin a / sin (L - a) - K = 0
that's the correct a (angle ABC)

[Mighty Midget]

Sorry for the double, just want to keep things tidy in a messy topic



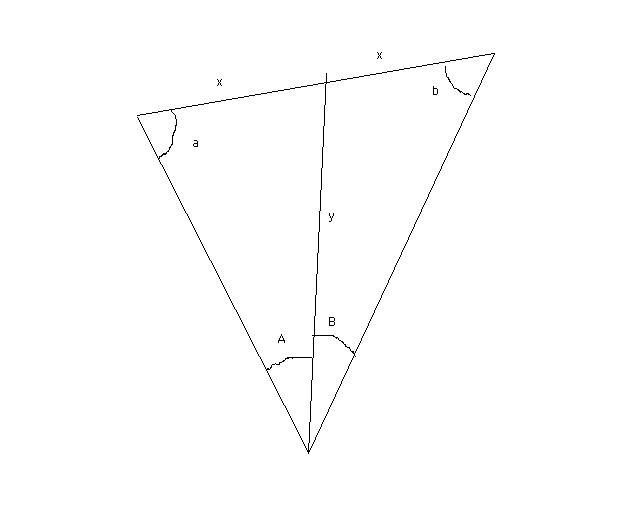x / sin A = y / sin a

x = y sin A / sin a

----

x / sin B = y / sin b

x = y sin B / sin b

----

since x = x

sin A / sin a = sin B / sin b

sin A / sin B = sin a / sin b

sin A / sin B = K

b = 180 - (A + B) - a

180 - (A + B) = L

K = sin a / sin (L - a)

sin a / sin (L - a) - K = 0

[DoomYoshi]

Originally Posted by Mighty Midget

The "IRL" problem was: At time t = 0 I had a ship at bearing x. 3 minutes later the bearing had changed to y, and 3 minutes later the bearing was z. From these data I wondered if I could calculate the ship's course.

Did the ship maintain the same speed? Does the game provide velocity? How do you know the value of the angles?

[AlumiuN]

Gaaah? Why bring up trig? *calms down a little* Sorry, I had a Maths common test this morning. I've done enough differentiation for one day.

[Mighty Midget]

Sorry for the late reply.

Doom: The angles A and B on the last diagram are calculated from 3 readings of the bearing to the ship. A and B are the difference between the 3 readings.

Also, the speed is assumed to be constant, as is the heading.

[Tomekk]

Ohh God, schools only 1 week, and i have to repeat all this shit!

[Japo]

I didn't read through the whole topic... You just have to state the simple relationships (equations 1 and 2) between the three angles formed by e with b, c and d (gamma, delta and epsilon in my notation). Then you use the BC=CD equation and presto, I think using the law of sines is the simplest option.

[Mighty Midget]

Thanks a bunch, Japofran! I will look into this, but it looks promising.

Ok, here's another one:

From a defined point on Earth, you know your distance from that point as well as your bearing as seen from that point (that is, if you are due east of that point, you are at bearing 90 degrees, if you are due north, your bearing is 360, and so on). If your coordinates are 136 70, you are at bearing 136 (South East) at a distance of 70 (be it mm, metres, miles or whatever) from the point.

Your coordinates are [b d] (b being bearing, d being distance)

You also know your own heading h, that is which direction you're facing i.e. 25 degrees (North North East).

You are then to move from coordinates [b d] to a new location given by the coordinates [B D]

What is your new heading H, how many degrees will you have to turn and in which direction (smallest angle), and what is the distance from [b d] to [B D]?